728x90
728x90
Graph
- A collection of nodes and arcs to represent a structure
- Objects: A finite set of nodes (or vertices ,points)
- Relationship: A finite set of arcs (or edges, links)
- Formally, a graph is denoted by G = (V,E).
- V: a set of vertices
- E: a set of edges, a set of 2-elements of V
- In general, a graph may have parallel edgesand self loops.
- But, Simple graph don't have parallel edges and self loops.
- Assume that the graph is simple unless otherwise specified.
- Edges may be associated with "weighted" values.

- Undirected graph
- Vertices on edges form unordered pairs.
- The order of vertices in edges is not important.
- (u, v) means there is an edge between u and v.
- Directed graph (aka. digraph)
- Edges have a direction.
- Vertices on edges form ordered pairs.
- The order of vertices in edge is important.
- (u, v) means there is an edge from u to v.

undirected grpah(left), directed graph(right)
- Degree of a vertex in undirected graphs.
- The number of edges incident to the vertex
- The number of edges = (sum of degree of all vertices) / 2
- For diagraphs, there are two types: indegree and outdegree
- indegree: the number of incoming edges incident on a vertex in a directedgraph
- outdegree: the total number of edges emanating from that node

- Adjacent vertex
- A vertex u is said to be adjacent to another vertex v in G if the graph contains an edge (u, v)
- Path from a vertex u to another vertex v in G
- A sequence of vertices, u, v1, v2, ..., vk, v where (u, v1), (v1, v2), ... , (vk, v) are edges in G
- Length of a path: The number of edges between u and v
- Simple path: A path that does not have redundant edges
- Cycle: A path where the starting and ending vertices are same.
- Connected Graph
- In undirected graph G, u and v are connected if there is a path from u and v.
- if any vertex in G is connected to any other vertices, it is said that graph G is connected.
- A graph in which a path exists between all two vertices.
- connected component: A maximal connected subgraph
- Complete Graph
- A graph of which all vertices are adjavent to any other vertices.
- Undirected graph: n(n - 1)/2 edges
- Directed graph: n(n - 1) edges
- Dense graph(밀집 그래프)
- Has many edges |E| ≈ |V|
- 간선(변)의 수가 최대 간선의 수에 가까운 그래프
- Represented as an adjacency matrix
- Sparse graph(희소 그래프)
- Has few edges |E|<<|V|^2 or |E| ≈ |V|
- 간선이 얼마없는 그래프
- Represented as an adjacency list
- Subgraph
- Subgraph G' = (V', E') of graph G = (V, E). A graph such that 𝑽′ ⊆𝑽and𝑬′ ⊆𝑬
- A graph of which all vertices are adjavent to any other vertices.
- The complexity of graph algorithms is typically defined in tersm of Number of vertices |V|, Number of edges |E|, or both
- Graph traversal
- Depth first search(DFS)
- Breadth first search(BFS)
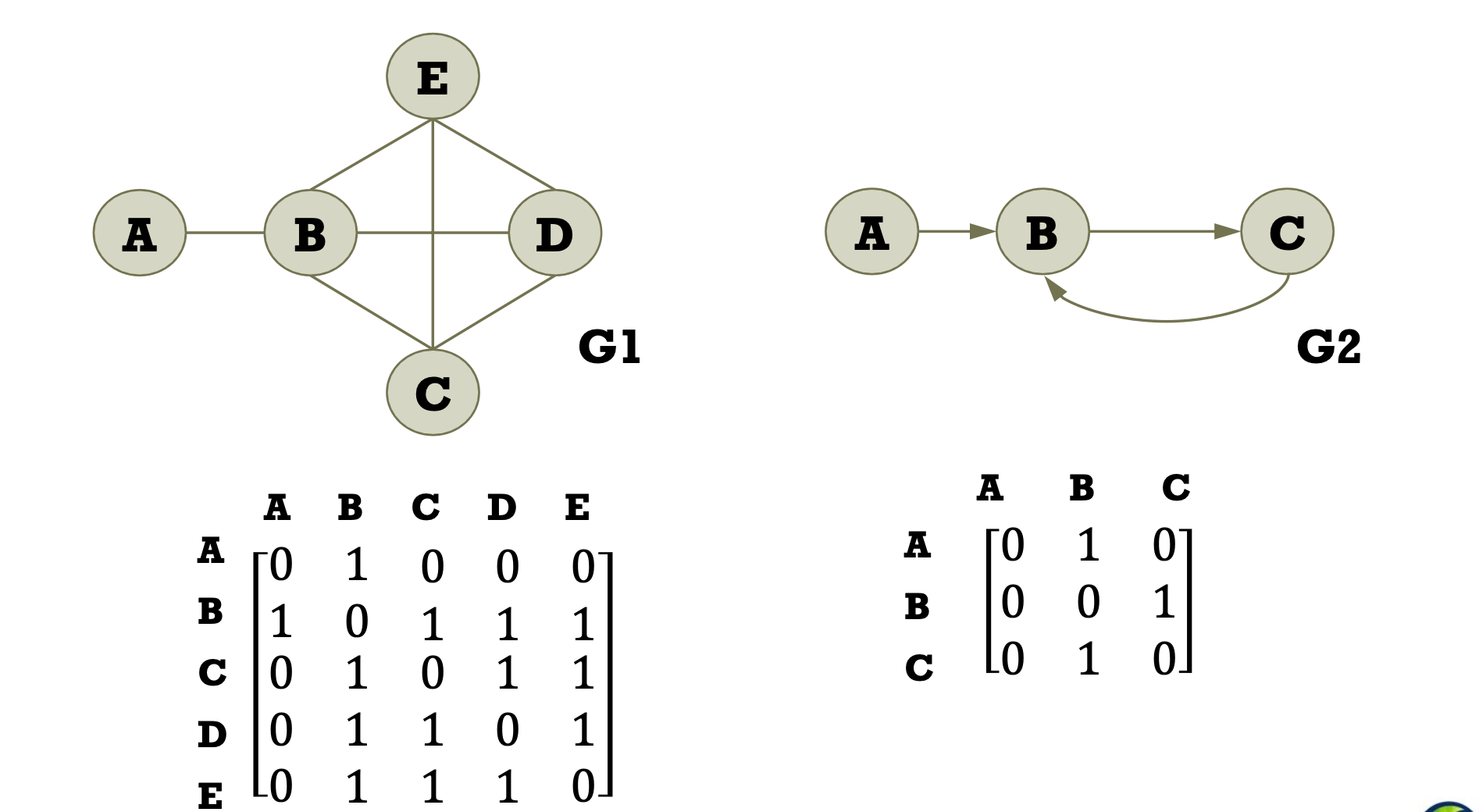
- Graph represented by adjacency matrix
- Allocate |V| X |V| matrix M.
- M[i][j] = 1 if there is an edge between vi and vj
- M[i][j] = 0 if there is not an edge between vi and vj
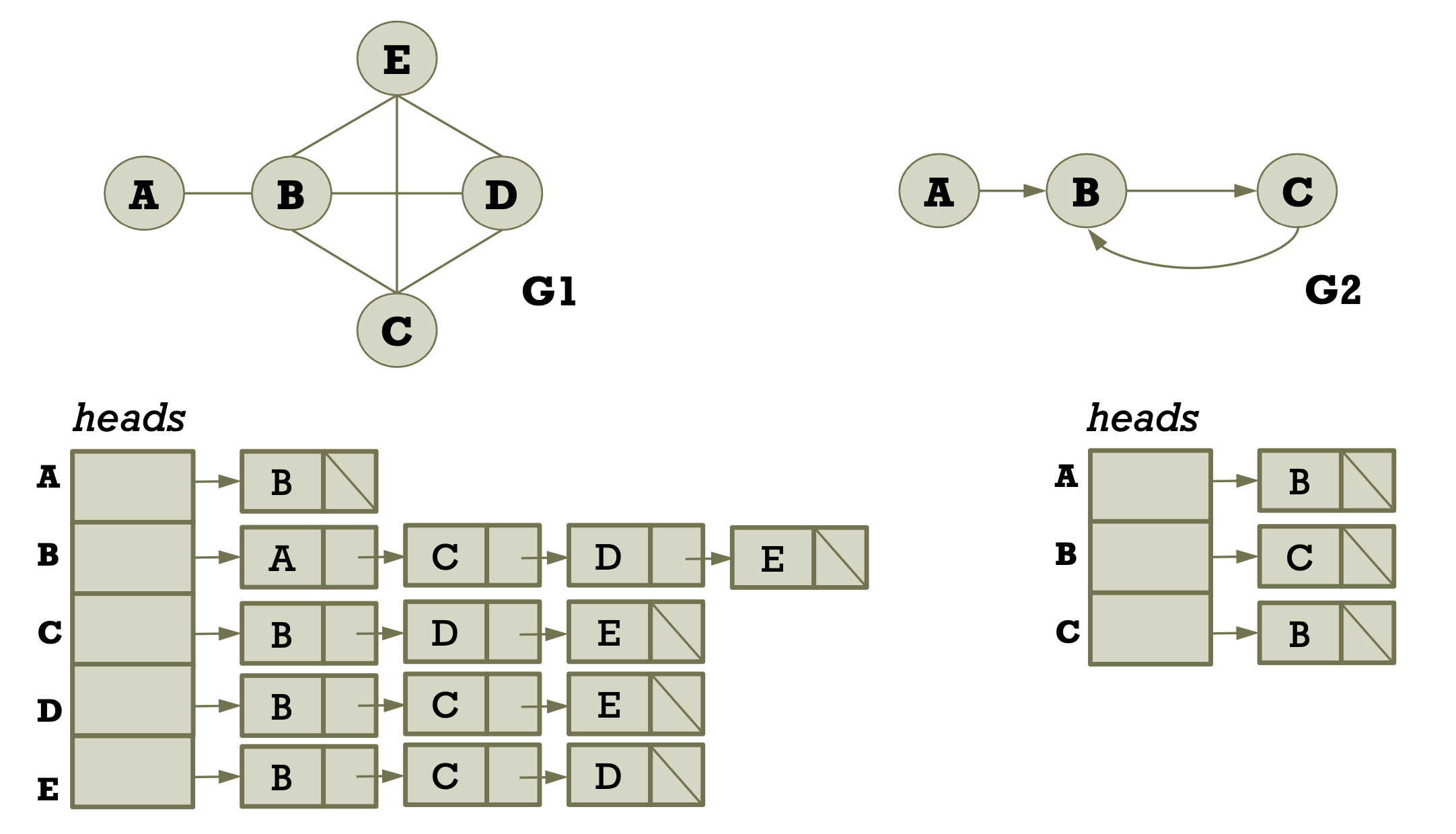
- Graph represented by adjacency list
- Allocate an array called heads
- heads[i] points to a linked list of nodes connected to vi
// GNode: It is connected from each ehad pointer.
typedef struct _GNode
{
int id;
struct _GNode* next;
}
// Graph: heads are GNode pointers.
typedef struct
{
int num;
GNode** heads;
} Graph;
// Create a graph.
void CreateGraph(Graph* pgraph, int num);
// Destroy a graph.
void DestroyGraph(Graph* pgraph);
// Add an undirected edge from src to dest.
void AddEgde(Graph* pgraph, int src, int dest)
// Print a graph for each vertex.
void PrintGraph(Graph* pgraph);
// Depth first search
void DFS(Graph* pgraph);
// Breadth first search
void BFS(Graph* pgraph);
void CreateGraph(Graph* pgraph, int num(
{
pgraph->num = num;
pgrap->heads = (GNode **)malloc(sizeof(GNode*)* num);
for (int i = 0; i < num; i++){
//Make a dummy node.
pgraph->heads[i] = (GNode *)malloc(sizeof(GNode));
pgraph->heads[i]->next = NULL;
}
}
void DestroyGraph(Graph* pgraph)
{
for(int i = 0; i < pgraph->num; i++){
GNode* cur = pgraph->heads[i];
while (cur != NULL){
GNode* temp = cur;
cur = cur->next;
free(temp);
}
}
}
void AddEdge(Graph* pgraph, int src, int dest)
{
GNode* newNode1, *newNode2, *cur;
newNode1 = (GNode *)malloc(sizeof(GNode));
newNode1->id = dest;
newNode1->next = NULL;
cur = pgraph->heads[src]; // Create a node for dest in src.
while (cur->next != NULL)
cur = cur->next;
cur->next = newNode1;
newNode2 = (GNode *)malloc(sizeof(GNode));
newNode2->id = src;
newNode2->next = NULL;
cur = pgraph->heads[dest]; // Create a node for src in dest.
while (cur->next != NULL)
cur = cur->next;
cur->next = newNode2;
}- Also, you can use another heads for columns like this.

728x90
300x250
'Computer Science > Data Structure' 카테고리의 다른 글
| [Data Structure] 리스트(List) (0) | 2023.12.26 |
|---|---|
| [Data Structure] 큐(Queue) (0) | 2023.12.26 |
| [Data Structure] 스택(stack) (0) | 2023.12.26 |
| [Data Structure] 자료구조와 알고리즘 (0) | 2023.12.26 |