728x90
728x90
Quick Sort
- Based on the divide and conquer(D&C) paradigm.
- Overall procedure
- Pivot selection: Pick an element, called a pivot, from the list.
- ex) For each list, select a pivot as the left-most element.
- Partitioning: reorder the list with the pivot.
- The elements less than the pivot come before the pivot.
- The elements greater than the pivot come after the pivot.
- ex) Partitino the list into two sublists.
- Recursively apply the above steps to the sublists.
- Pivot selection: Pick an element, called a pivot, from the list.
- Use two variables
- low: if L[low] is less than a pivot, move to the right element.
- high: if L[high] is greater than a pivot, move to the left element.
- After find the low and high, swap two elements L[low] and L[high].
- If low and high are crossed, stop partitioning. and swap into element L[left] and L[high].
- Assume that the left-most element is the pivot.
- left: an starting index for a sublist that is less than a pivot.
- right: an ending index for a sublist that is greater than a pivot.
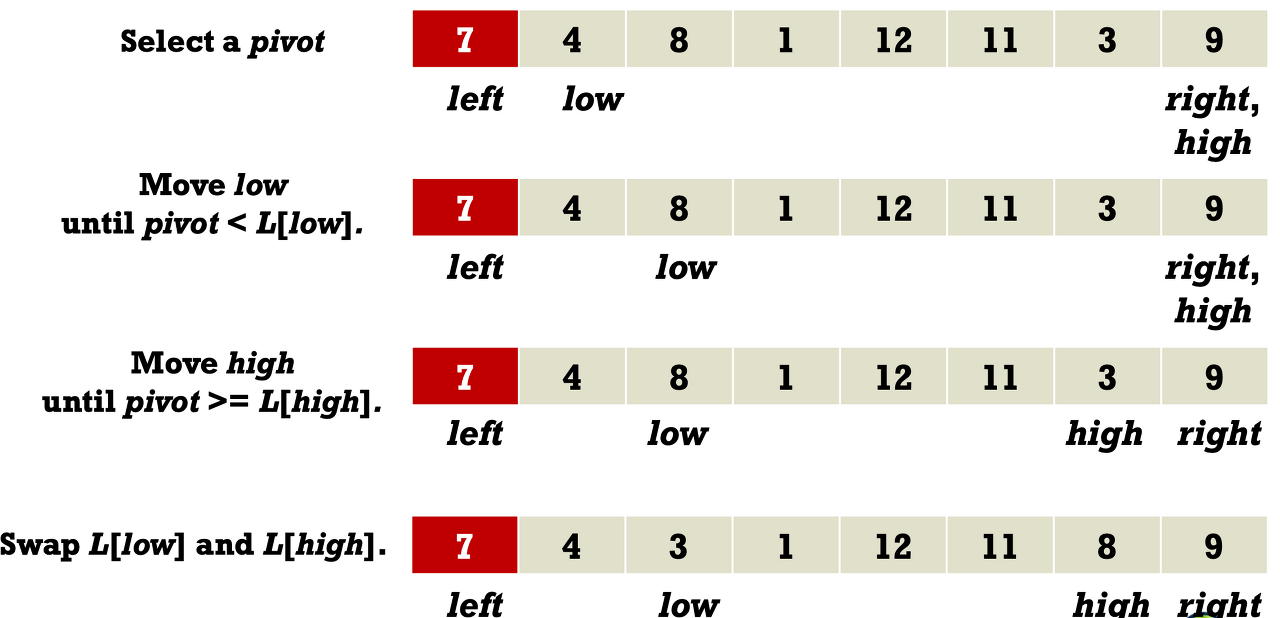
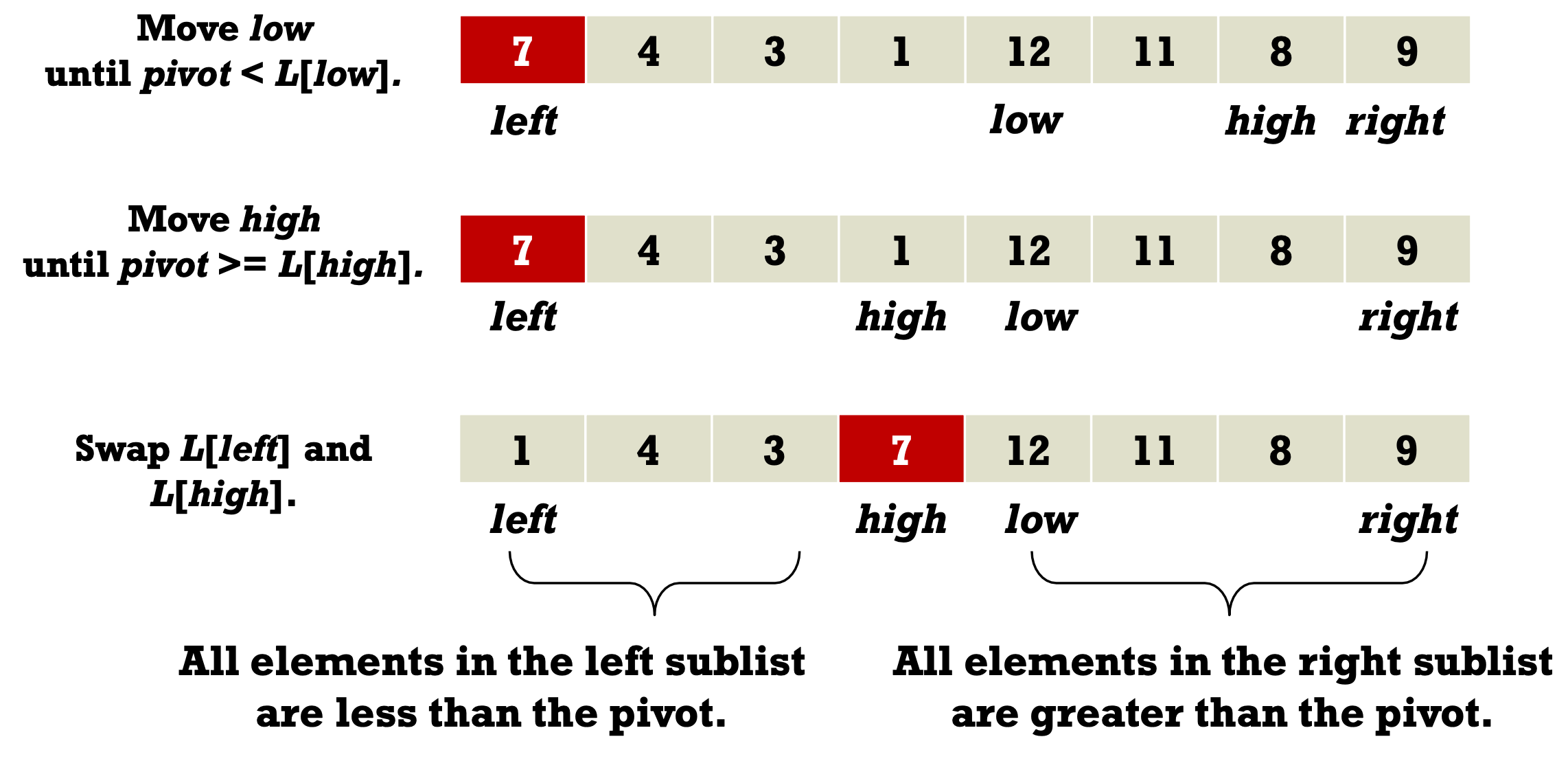
- Partitioning one list into two sublists.
- All elements in the left sublist are less than the pivot.
- All elements in the right sublist are greater than the pivot.
/*
for each (unsorted) partition
set first element as pivot
storeIndex = pivotIndex+1
for i = pivotIndex+1 to rightmostIndex
if ((a[i] < a[pivot]) or (equal but 50% lucky))
swap(i, storeIndex); ++storeIndex
swap(pivot, storeIndex-1)
*/
int Partition(Data* list, int left, int right)
{
int pivot = list[left], temp;
int low = left + 1, high = right;
while(1)
{
while (low < right && list[low] < pivot)
low++; // Move low until pivot < L[low]
while (high > left && list[high] >= pivot)
high--; // Move high until pivot >= L[low]
if (low < high)
// Swap list[low] and list[high]
SWAP(list[low], list[high], temp);
else break;
}
SWAP(list[left]. list[high], temp);
return high; // return the pivot position.
}
void QuickSort(Data* list, int left, int right)
{
if (left < right)
{
// The mid refers to the pivot posittion.
int mid = Partition(list, left, right);
// All elements are less than the pivot.
QuickSort(list, left, mid - 1);
// All elements are greater than the pivot.
QuickSort(list, mid + 1, right);
}
}- We expect that the list will be split into two halves in an average case
- 𝑻 (𝒏) =𝟐𝑻 (𝒏/2) +𝒄𝒏, where splitting time is cn.
- By the master theorem, it is 𝑂(𝑛log 𝑛).
- The time complexity of quick sort is 𝑂(𝑛log 𝑛).
- However, the worst case is that the list will be split into 1 and n - 1.
- T(n) = T(n - 1) + cn = T(n - 2) + 2cn = ... = T(1) + cn(n -1) = O(n^2)
- The time complexity of quick sort is O(n^2)
- The worse case occurs if the pivot is selected as an extremely skewed case.
- The time complexity of quick sort mainly depends on pivot selection.
728x90
300x250
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Divide and Conquer(D&C) Paradigm (0) | 2023.12.26 |
|---|---|
| [Algorithm] Shell sort (0) | 2023.12.26 |
| [Algorithm] Bubble sort (0) | 2023.12.26 |
| [Algorithm] Selection sort (0) | 2023.12.26 |
| [Algorithm] Sorting algorithm (0) | 2023.12.26 |