728x90
반응형
Division
- 알고리즘
- partial remainder > divisor -> quotient bit = 1, remanider = remainder - divisor
- partial remainder < disivor -> quotient bit = 0
- 다음 비트로 이동
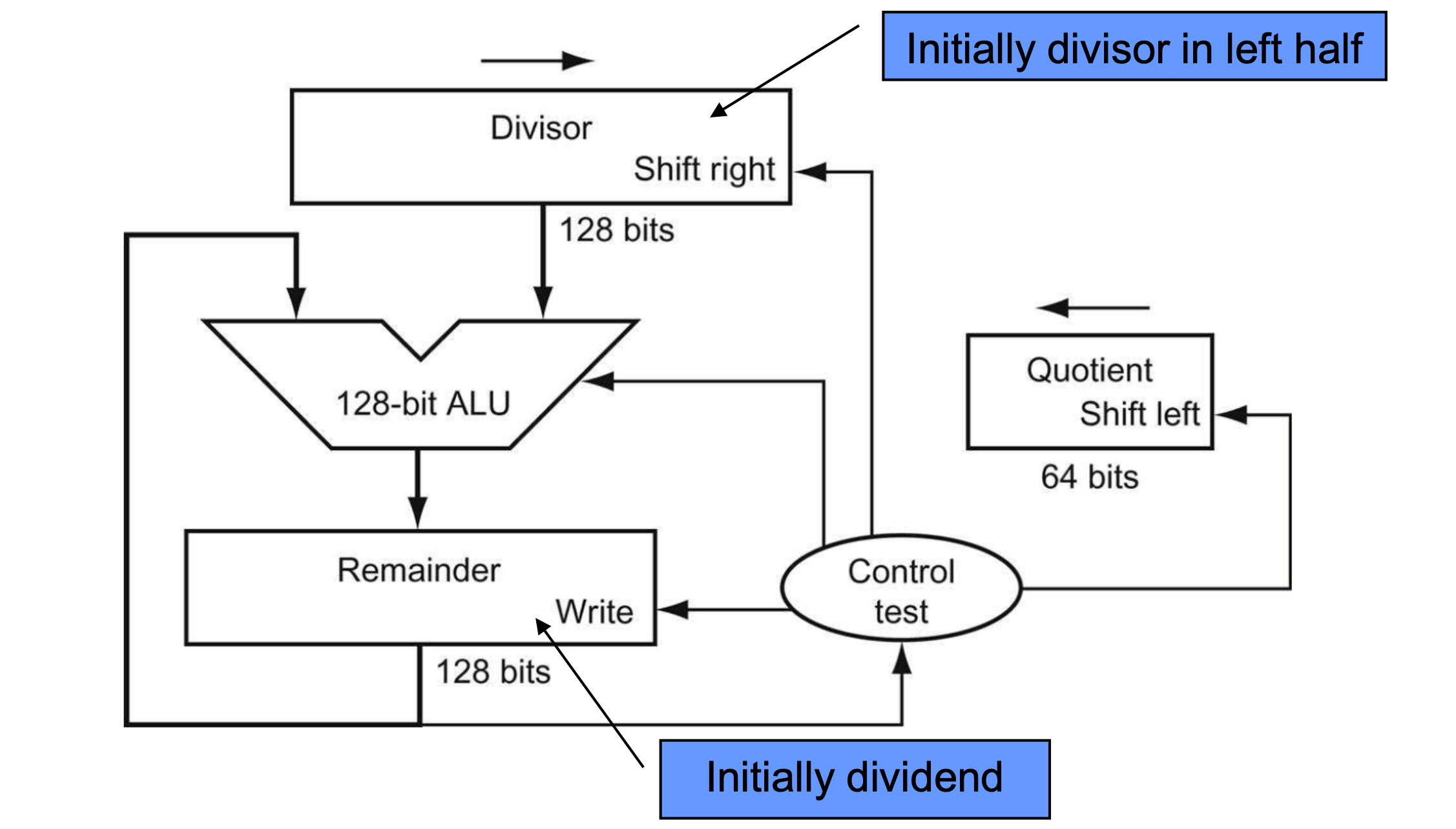
- Divisor는 처음에는 맨 왼쪽 값을 쓰다가 점점 오른쪽으로 이동하면서 빼야하기 때문에 128bit
- 뺀 결과가 양수면 Quotient에 1을 넣고, 음수면 1을 넣는다. 왼쪽으로 shift하는데, 음수가 나왔을 때는 다시 원상 복귀한다.
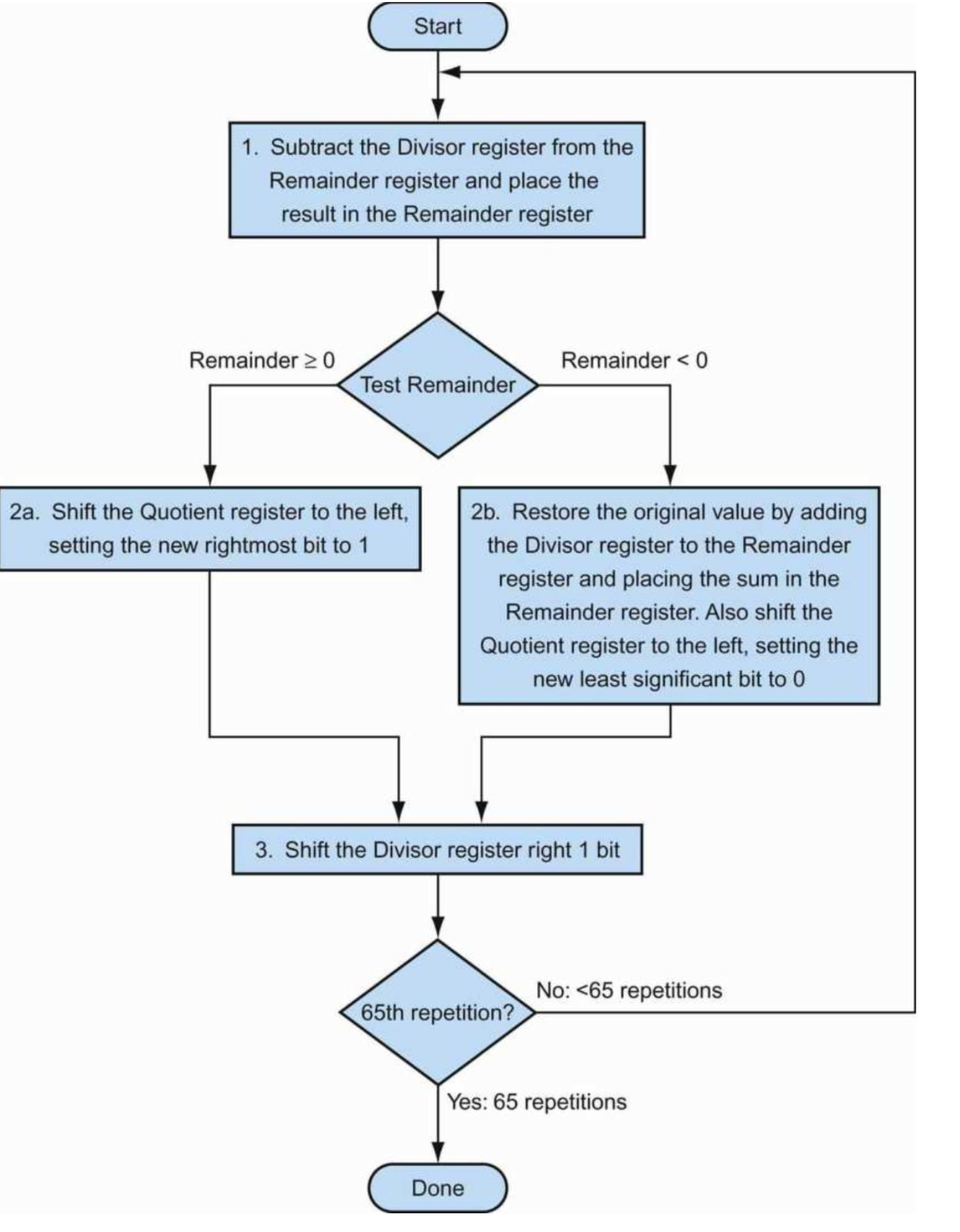
- N-bit Quotient와 Remainder를 처리하기 위해서는 N+1번 반복해야 한다. (multiplication은 N번 반복이었음)

- Iter 0
- 3비트 연산이기에 Remainder, Diviosr는 6bit, Quotient는 3bit로 설정합니다.
- Remainder 7은 아래 3bit에, Divisor 3비트는 상위 3bit 위치시킵니다.
- Iter 1
- Remainder - Divisor를 합니다.
- 결과값 101111의 signed bit가 1이므로 음수 -> 원상복구
- Quotient는 왼쪽으로 1bit 이동시킵니다.
- Divisor를 오른쪽으로 1bit 이동시킵니다.
- Iter 2
- Remainder - Divisor를 합니다.
- Quotient는 왼쪽으로 1bit 이동시킵니다.
- 결과값 111011의 signed bit가 1이므로 음수 -> 원상복구
- Divisor를 오른쪽으로 1bit 이동시킵니다.
- Iter 3
- Remainder - Divisor를 합니다.
- Quotient는 왼쪽으로 1bit 이동시킵니다.
- 결과값 000001의 signed bit가 0이므로 양수 -> Quotient의 가장 오른쪽 값은 1
- Divisor를 오른쪽으로 1bit 이동시킵니다.
- Iter 4
- Remainder - Divisor를 합니다.
- Quotient는 왼쪽으로 1bit 이동시킵니다.
- 결과값 111110의 signed bit가 1이므로 음수 -> 원상복구
- Divisor를 오른쪽으로 1bit 이동시킵니다.
Observations on Divison
- Divisor의 절반은 항상 0이다.
- 128bit adder의 절반과 divisor의 절반이 항상 낭비
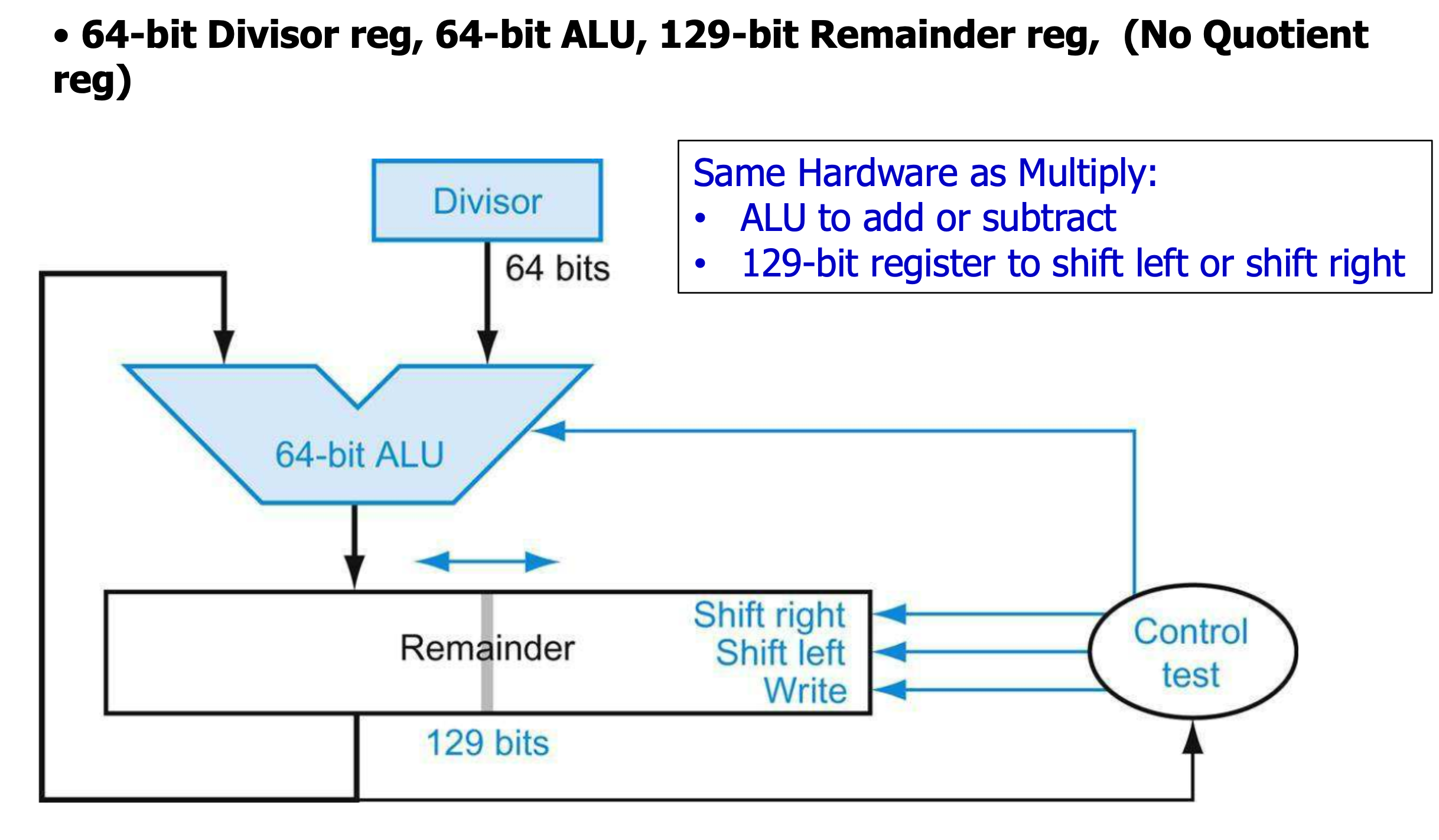
- Divisor를 오른쪽으로 shift하는 대신에 Remainder를 왼쪽으로 shift 하자!
- Divisor register는 64bit로 두면서
- 항상 첫 번째 단계에서는 Quotient bit가 1이 나올 수 없다. (Remainder - Divisor)를 하면 음수가 나오게 된다.(bit자리에 맞춰서)
- 만약 1이 나온다면 그건 Quotient가 너무 크다는 뜻
- 그래서 처음에는 검사를 하지않고 먼저 shift를 하고 2번째 iter부터 시작을 하자! -> 1번의 반복을 아낄 수 있다.
- Remainder는 매 사이클마다 1 bit씩 잃고, Quotient는 1bit씩 얻는다.
- 둘을 합쳐서 한꺼번에 왼쪽으로 shift시키자!
- 둘이 합치게 되면 Remainder는 기존보다 1번 더 shift되는 것이 되버린다. 그렇기 때문에 모든 반복을 마친 후에 Remainder Register만 한 번 오른쪽으로 shift시켜서 값을 유지시켜 주어야 한다.
Imporved Version of Divison
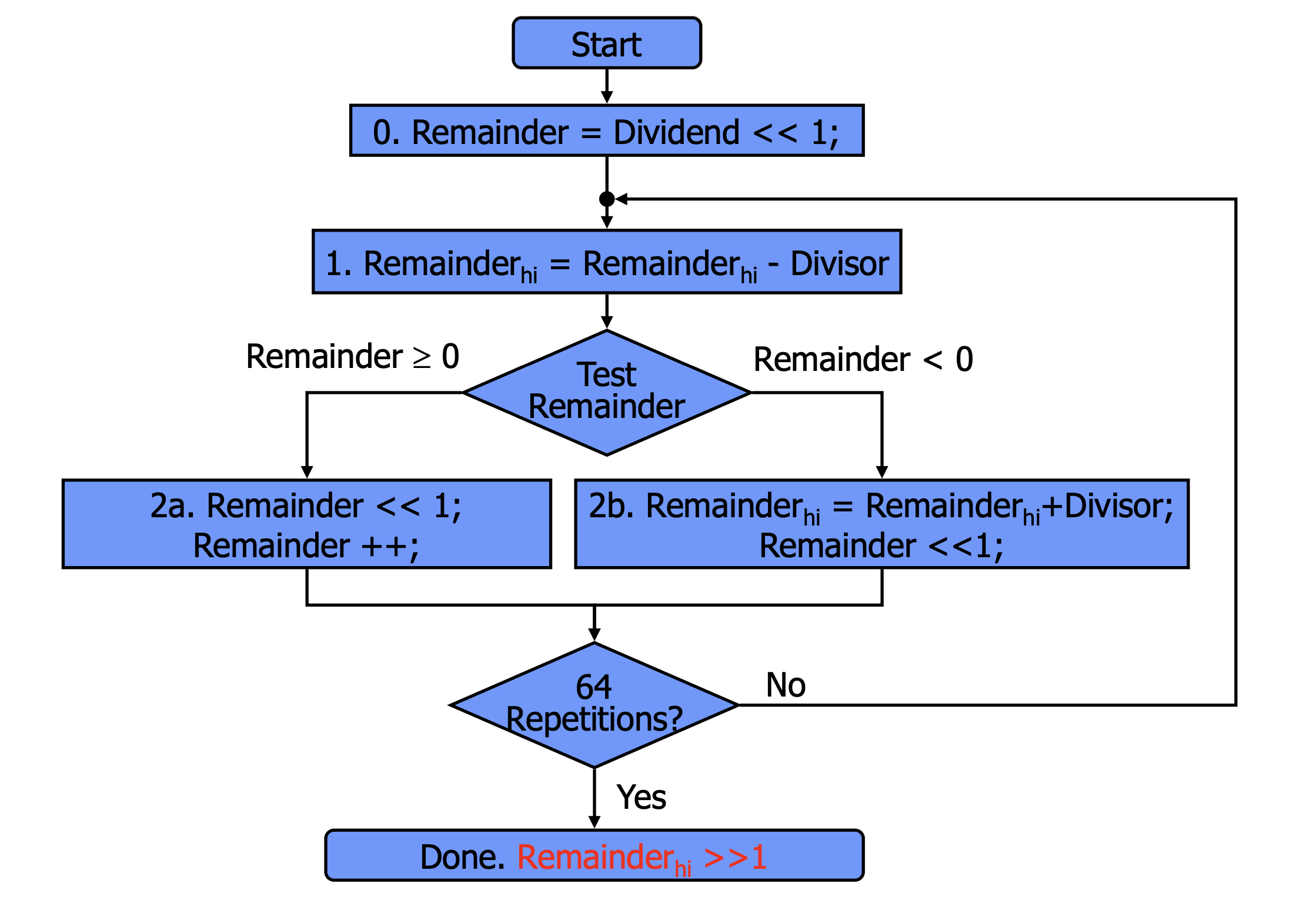

- Iter 0
- 4bit 나눗셈 연산
- 14는 0b1110이므로 처음에 Remainder는 0000 1110인데, 항상 첫 번째 Quotient bit는 0이므로 1bit shift한 상태로 시작을 합니다. 그래서 0001 1100입니다.
- Divisor 3은 0b0011입니다.
- 4bit 나눗셈 연산
- Iter 1
- Remainder의 상위 4bit에 Divisor를 뺍니다.
- signed bit가 1이므로 음수입니다.
- 원상복귀 후 왼쪽으로 한 칸 shift 합니다. 음수였기에 맨 오른쪽에 추가되는 값은 0입니다.
- Iter 2
- Remainder의 상위 4bit에 Divisor를 뺍니다.
- signed bit가 0이므로 양수입니다.
- 뺄셈을 한 값을 유지한 채로 왼쪽으로 한 칸 shift 합니다. 양수였기에 맨 오른쪽에 추가되는 값은 1입니다.
- Iter 3
- Remainder의 상위 4bit에 Divisor를 뺍니다.
- signed bit가 1이므로 음수입니다.
- 원상복귀 후 왼쪽으로 한 칸 shift 합니다. 음수였기에 맨 오른쪽에 추가되는 값은 0입니다.
- Iter 4
- Remainder의 상위 4bit에 Divisor를 뺍니다.
- signed bit가 1이므로 음수입니다.
- 원상복귀 후 왼쪽으로 한 칸 shift 합니다. 음수였기에 맨 오른쪽에 추가되는 값은 0입니다.
- 4번의 반복이 끝난 후에 Remainder Register의 왼쪽 4bit가 Remainder, 오른쪽 4bit가 Quotient가 됩니다. Remainder는 한 번 더 왼쪽으로 shift된 상태이므로, 오른쪽으로 1번 shift를 해줍니다.
Nonrestoring Divison
- Dividend = Quotient x Divisor + Remainder
- +7 / + 2 = 3 x 2 + 1
- -7 / +2 = -3 x 2 -1
- -7 / +2 = -4 x 2 + 1 (x) 나눠지는 숫자(Dividend)와 나머지(Remainder)는 같은 부호를 가져야합니다!
- Quotient negated
- 나누는 숫자(Divisor)의 부호와 나눠지는 숫자(Dividened)의 부호가 일치하지 않을 때
- 지금 까지는 (r + d) x 2 - d 로 Restore(+d) 후 Subtract(-d)를 했습니다.
- (r + d) x 2 - d = r x 2 + d x 2 - d = r x 2 + d이므로 restore를 하지않고 d를 더해주어도 일치하게 됩니다.
- 2를 곱하는 과정을 먼저 처리 후(왼쪽으로 shift) d를 더하는 식으로 하면 restore 과정을 거치지않아도 됩니다.
- restore를 하지않고 그 전의 결과가 음수라면 왼쪽으로 shift를 한 다음에 divisor를 더하자!
- 나누는 숫자(Divisor)의 부호와 나눠지는 숫자(Dividened)의 부호가 일치하지 않을 때


- Iter 0
- 4bit 나눗셈 연산
- 14는 0b1110이므로 처음에 Remainder는 0000 1110인데, 항상 첫 번째 Quotient bit는 0이므로 1bit shift한 상태로 시작을 합니다. 그래서 0001 1100입니다.
- Divisor 3은 0b0011입니다.
- 4bit 나눗셈 연산
- Iter 1
- Remainder의 상위 4bit에 Divisor를 뺍니다.
- 음수가 나왔지만 restore를 하지않고 그 상태 그대로 왼쪽으로 shift를 합니다.
- 음수이기에 새롭게 추가되는 bit(맨 오른쪽)은 0입니다.
- Iter 2
- Iter1에서의 결과가 음수였기에 Remainder의 상위 4bit에 Divisor를 더합니다.
- 값의 결과는 양수입니다. 그 상태 그대로 왼쪽으로 shift를 합니다.
- 양수이기에 새롭게 추가되는 bit(맨 오른쪽)은 0입니다.
- Iter 3
- Iter2의 결과가 양수였기에 Remainder의 상위 4bit에 Divisor를 뺍니다.
- 음수가 나왔지만 restore를 하지않고 그 상태 그대로 왼쪽으로 shift를 합니다.
- 음수이기에 새롭게 추가되는 bit(맨 오른쪽)은 0입니다.
- Iter 4
- Iter1에서의 결과가 음수였기에 Remainder의 상위 4bit에 Divisor를 더합니다.
- 그 결과는 1111 0010으로 음수입니다.
- 마지막 단계이면서 마지막 결과값이 음수이므로 restore를 한 번 합니다.(Divisor를 한 번 더 더해줌) (Dividend는 Remainder와 부호가 같아야 하므로)
- 그 결과가 음수입니다. 왼쪽으로 shift하고 추가되는 새로운 bit는 0입니다.
- Remainder를 나타내는 상위 4비트만 오른쪽으로 1번 shift 해주어서 한 번 더 계산된 것을 복구해줍니다.
Floating Point
- sign(부호): 1이면 음수, 0이면 양수
- exponent(지수): exponent에 많이 할당할 수록 표현할 수 있는 수의 크기 증가
- significand(유효숫자, Mantissa(가수)): significand에 많이 할당할 수록 accuracy 증가
IEEE 754 Floating Point

- Mantissa(가수)는 1.xxxx 형태로 정규화를 한 뒤 가장 왼쪽에 있는 1을 제거하고 소수점 이하의 자리 값만 표현
- 항상 맨 앞에 1이 있다고 가정을 해서 굳이 처음 1bit를 표현안해도 된다. (1 bit 아낌)
- 모든 유효숫자는 1. 으로 시작하는 수로 바꿀 수 있다.
- 예를 들어, 0.01011 -> 1.011 x 2^(-2)으로 맨 앞에 1로 시작하도록 바꿀 수 있다.

- bit를 부여할 때, exponent가 앞에 오는 이유?
- sorting을 편하게 하기 위해서!
- 일반적으로 exponent가 클수록 수가 더 크기 때문이다.
- 따라서 exponent를 앞에 배치함으로써 두 숫자를 비교할 때, 앞쪽만을 비교하고 앞쪽이 더 크면 더 큰 숫자를 나타낸다고 판단하여 계산과정을 줄이며 sorting을 할 수있음
728x90
반응형
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] Datapath (0) | 2024.02.29 |
|---|---|
| [Computer Architecture] Clocking Methodology (1) | 2024.02.29 |
| [Computer Architecture] Multiplication for computers (1) | 2024.02.28 |
| [Computer Architecture] RISC-V overflow (1) | 2024.02.27 |
| [Computer Architecture] Arithmetic Logic Unit(ALU, 산술 논리 장치) (1) | 2024.02.27 |