728x90
728x90
Integer Multiplication

- m bits x n bits -> 계산결과는 (m+n) bit
- Binary rules
- 0이면 0을 쓴다. (0 x multiplicand)
- 1이면 multiplicand를 그대로 쓴다. (1 x multiplicand)
- 1 clock per step -> ~ 200 clocks per multiply
- add보다 multiply는 frequency가 낮다.
- multiply는 Amdahl's law에 따르면 uncommon case이다.
Multiplication - 1

- Multiplier를 오른쪽으로 shift해가면서 하드웨어는 Multiplier의 가장 오른쪽 bit를 하나씩 검사하고 그 값에 따라 제어합니다.
- ex) Multiplier 1001 -> 가장 맨 오른쪽 값이 1이구나 -> right 1 shift -> 0100 -> 가장 맨 오른쪽 값이 0이구나
- Product는 0으로 시작합니다. (검사하면서 값을 계속 업데이트)

- 11 x 9 multiplcation 예시

- Iter 0
- 11과 9 모두 4bit로 표현가능 하므로 4bit 장치라고 가정
- 4bit * 4bit -> 8bit 결과이므로 product는 8bit
- multiplicand는 왼쪽으로 값을 옮겨갈 것이므로 8bit로 준비
- product 초기값은 0
- multiplicand는 11이므로 00001011
- multiplier는 9이므로 1001
- Iter 1
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 1
- multiplicand를 product에 더한다.
- 더한 뒤에 multiplicand는 1bit left shift, multiplier는 1bit right shift
- multiplicand: 00010110
- multiplier: 0100
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 1
- Iter 2
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 0
- product에 아무동작도 하지 않는다.
- multiplicand는 1bit left shift, multiplier는 1bit right shift
- multiplicand: 00101100
- multiplier: 0010
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 0
- Iter 3
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 0
- product에 아무동작도 하지 않는다.
- multiplicand는 1bit left shift, multiplier는 1bit right shift
- multiplicand: 01011000
- multiplier: 0001
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 0
- Iter 4
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 1
- multiplicand를 그대로 product에 더한다.
- 더한 뒤에 multiplicand는 1bit left shift, multiplier는 1bit right shift
- multiplicand: 10110000
- multiplier: 0000
- multiplier의 가장 오른쪽 bit, 즉 2^0자리 bit가 1
- 4bit 연산이었으므로 4번의 반복을 하고 종료한다.
Observations on Multiplication
- multiplicand의 절반(불연속적)은 항상 0bit로 채워져 있다.
- 절반이 항상 낭비가 되므로 비효율적
- mutiplicand를 오른쪽으로 shift하기 위해서 0을 삽입하고 있다.
- product의 LSBs(Least Signficant bit)는 한 번 생성되면 바뀌지 않는다.
- 처음에 multiplicand의 왼쪽 절반과 product는 다 0이라 값이 변하지않는다.
- 이 점을 이용해서 비효율적으로 0을 삽입하는 것을 줄일 수 있다
- mutliplicand를 왼쪽으로 shift하는 것이 아니라 product를 오른쪽으로 shift하자!
- 근데 이렇게 하니까 product register의 lower half는 모두 0bit로 채워져있기에 공간을 낭비한다.
- product register와 multiplier register를 합치자! (둘 다 오른쪽으로 shift하므로)
Multiplication - 2
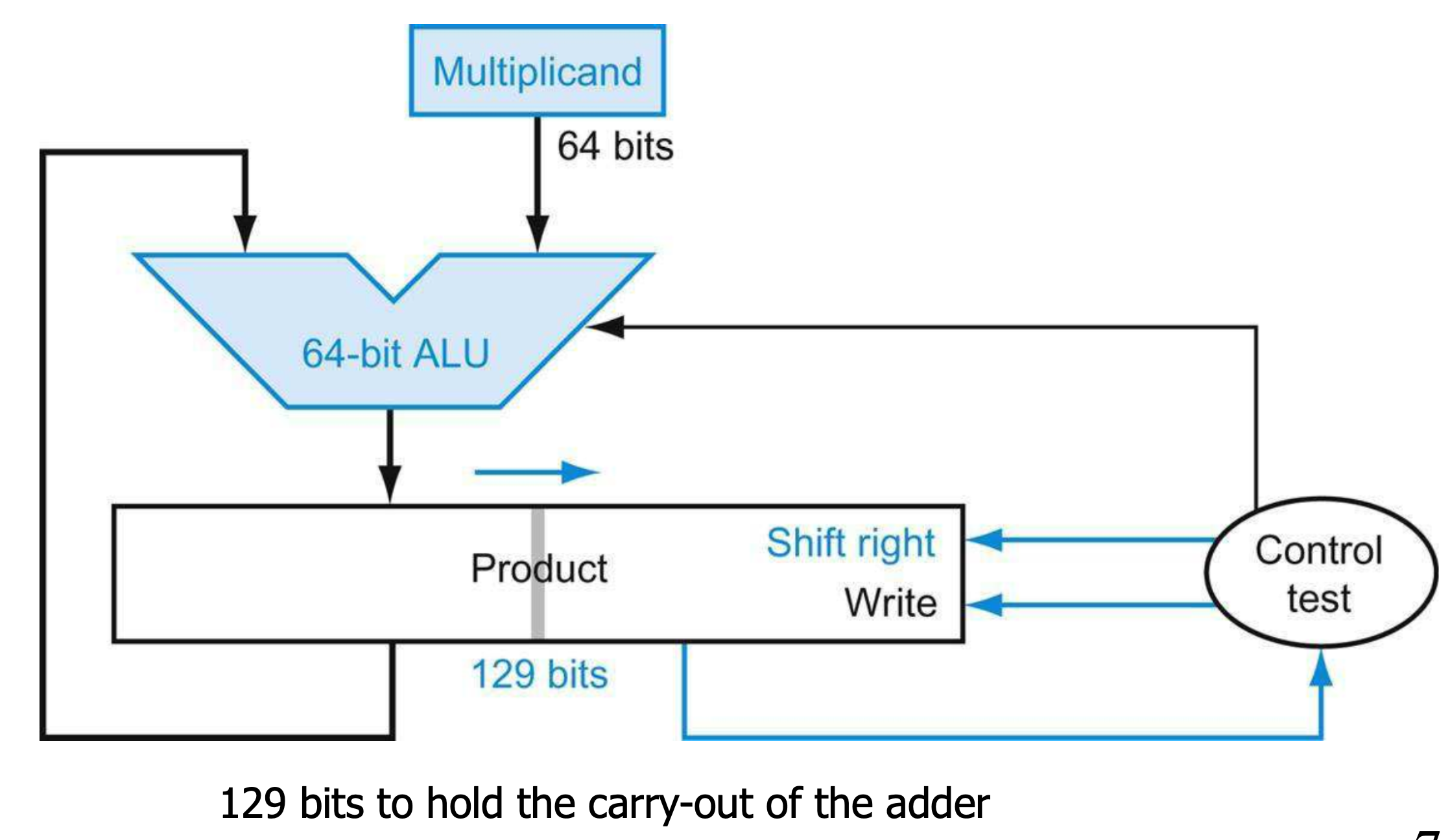
- 두 개의 register를 더하는 과정에서 carry가 발생할 수 있는데 처음 버전에는 절반을 다 0으로 채워서 빈공간이 많았지만, 지금은 64, 64 bit씩 꽉꽉 채워서 쓰니까(원래 multiplier register로 따로 두었던 것을 합쳐 사용하기 때문) 빈 자리가 없기에 carry를 담는 1 bit를 추가해서 129bit product reg를 사용합니다.
- 11 x 9 multiplcation 예시

- Iter 0
- product의 맨 오른쪽 4 bit는 multiplier를 나타냄
- 어차피 계산이 끝나면 전체적으로 4 bit가 right shift되기 때문에 결과에 영향을 주지않음
- multiplicand는 4bit로 고정된 값
- product의 맨 오른쪽 4 bit는 multiplier를 나타냄
- Iter1
- product의 맨 끝 bit가 1이므로 product 앞 4bit에 multiplicand를 더함
- 더한 뒤에, product를 1 bit right shift
- Iter2
- product의 맨 끝 bit가 0이므로 그냥 넘어감
- product를 1 bit right shift
- Iter3
- product의 맨 끝 bit가 0이므로 그냥 넘어감
- product를 1 bit right shift
- Iter4
- product의 맨 끝 bit가 1이므로 product 앞 4bit에 multiplicand를 더함
- 더한 뒤에, product를 1 bit right shift
- 4bit 연산이므로 4번의 반복 끝난 후 종료
- 여기에는 안나타나있지만 carry위한 1개의 bit가 product에 추가로 있다. 더할 때 carry에 값을 잠시 가지고 있다가 오른쪽으로 shift할 때 적어준다.
Multiply in RISC-V
- RV32M/RV64M에서 지원
- RV32I는 multiply 지원하지 않는다(간단한 버전에서는 지원 x)
- 4 Instructions로 구성
- 128-bit product의 lower 64 bit를 얻는다.
- multiply (mul, rd, rs1, rs2): x[rd] = x[rs1] x x[rs2]
- 128-bit product의 upper 64 bit를 얻는다.
- multiply high (mulh): both operands are signed (signed shift), x[rd] = (x[rs1] s x s x[rs2]) >> s 64
- multiply high unsigned (mulhu): both operands are unsigned, x[rd] = (x[rs1] u x x[rs2]) >> u 64
- multiply high signed-usigned (mulhsu): signed/unsigned, x[rd] = (x[rs1] s x x[rs2]) >> s 64
- 128-bit product의 lower 64 bit를 얻는다.
- signed multiplication
- 전부 positive라고 가정하고 signed bit를 제외한 31bit에 대해 연산을 수행한다. 그 뒤에 둘의 부호가 다르면(signed bit) 결과값을 음수로 바꾼다.
- Better solution: Booth's Algorithm
- multiply two's complement signed numbers
- uses same hardware as before
- can also be used to reduce the numbers of steps
Booth Algorithm
- 0에서 1로 바뀔 때, 1에서 0으로 바뀔 때만 더하기 연산을 한다.


728x90
300x250
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] Clocking Methodology (1) | 2024.02.29 |
|---|---|
| [Computer Architecture] Division for computers (0) | 2024.02.29 |
| [Computer Architecture] RISC-V overflow (1) | 2024.02.27 |
| [Computer Architecture] Arithmetic Logic Unit(ALU, 산술 논리 장치) (1) | 2024.02.27 |
| [Computer Architecture] Arithmetic for computers (0) | 2024.02.08 |