- 가치평가와 현금흐름
1. 현금흐름 추정원칙
- 증분기준으로 추정: 투자안의 채택 시 해당 기업의 모든 변화가 분석에 포함
- 세후기준으로 추정: 감가상각에 따라 법인세가 달라지므로 감가상각비의 절세효과 고려
- 해당 투자안에 의한 모든 간접적 효과 고려
- 현금유입과 현금유출의 시점을 정확히 추정: 회계상 시점과 실제 시점의 차이 고려
- 기회비용은 고려대상이나 매몰비용(이미 투입된 회수 불가능비용)은 고려하지 않는다.
- 현금흐름 = 영업이익 X (1 - 법인세율) + 비현금비용(감가상각비 등)
2. 가치평가(Valuation)
자산으로부터 발생하는 미래현금흐름을 추정하고, 적정한 자본비용(k)으로 할인하여 자산의 현재가치를 추정하는 것을 말한다.
P = S / (1 + YTM)^n
자산의 현재가치는 만기상환금 또는 미래총현금흐름(S)을 적정할인율로 잔존기간만큼 할인한 것
- 현금유출: 재무상태표상의 '비유동자산, 유동자산, 유동부채'로부터 추정
- 현금유출 결정요인: 시설자금투자, 운전자본투자, 유동부채 -> '유무형자산의 증가 + 운전자본 - 비이자부 유동부채'로 추정
- 현금유입: 손익계산서상의 '영업이익'으로부터 추정
- 현금유입 결정요인: 손익계산서상의 영업이익 -> 투하자본은 본업활동을 통해 매출액으로 전환, 원재료비・인건비 등의 비용을 차감한후 영업이익을 창출함
* 비이자부 유동부채(Spontaneous Financing)는 외상매입금, 미지급금 등 이자비용을 부담하지 않고 조달하는 부채(운전자본의 현금유출을 줄여주는 역할을 함)
3. 현금흐름 측정기법
자금운용 접근법 = 자금조달 접근법
- 자금운용 접근법은 투자된 투하자본의 크기(BS의 차변) 위주로 측정하며, 자금조달 접근법은 부채와 자기자본 등 투하자본의 조달방법과 크기(BS의 대변)으로 측정한다.
- 증권분석을 위한 통계용어
1. 중심위치
- 산술평균: 모집단평균과 표본평균으로 구분
- 최빈값: 빈도수가 가장 높은 관찰치
- 중앙값: 관찰치를 순서대로 나열하였을 때 정가운데 있는 값
2. 산포경향
- 범위: 최대값 - 최솟값
- 평균편차: 각각이 평균으로부터 떨어진 거리들의 평균으로 측정
- 분산: 평균으로부터 떨어진 거리의 제곱들을 평균한 값
- 표준편차: 분산의 제곱근
3. 공분산
- 두 확률변수 간의 관계를 추정
- -∞ < 공분산 < +∞
- 공분산은 두 자산의 가격움직임 방향을 의미한다. 양이면 정의 방향, 음이면 반대 방향, 0이면 아무런 관계가 없음을 말한다.
4. 상관계수
- 두 변수의 관계의 방향과 정도를 나타내 주는 측정치로 공분산을 변수 각각의 표준편차로 나누어 준 값
- -1 < 상관계수 < 1
- 상관계수는 두 자산의 가격움직임의 방향뿐 아니라 그 정도를 나타낸다. 상관계수 값이 +1에 가까울수록 정비례 관계가 강해지며, -1에 가까워질수록 반비례 관계가 강해진다.
- 화폐의 시간적 가치
1. 단리와 복리
ex) 원금 100만 원, 연 4%, 만기 3년의 상품의 만기수령금액은(미래가치)?
- 단리: 100만 원(1 + 0.04 x 3)
- 연복리: 100만 원(1 + 0.04)^3
- 6개월 복리: 100만 원(1 + 0.04 / 2)^6
- 3개월 복리: 100만 원(1 + 0.04 / 4)^12
복리계산을 연 2회 이상할 경우의 미래가치: FV = PV x (1 + r/m)^(r*m)
ex) 원금 100만 원, 연 8%, 3개월 단위 복리, 만기 2년, 만기상환금액은?
FV = 100만 원(1 + 0.08/4)^(2x4) = 100만 원(1 + 0.08/4)^8
2. 실효연이자율
= (1 + r / m)^m - 1
m은 일년에 몇 번? (3개월이면 1년에 4번)
3. 복리요소 vs 현가요소
미래가치 FV = PV x (1 + r)^n
현재가치 PV = FV x 1/(1 + r)^n
복리요소(미래가치 이자요소) FVIF = (1 + r)^n
현가요소(현재가치 이자요소) PVIF = 1/(1 + r)^n
4. 연금(Annuity)
매 기간 적립하는 금액이 동일하고, 일정기간 연속적으로 일어난다.
선연금(Annuity Due)은 현금흐름이 매 기간 초에 발생하는 것이며, 보통연금(Ordinary Annuity)은 매 기간 말에 발생하는 것을 말한다.
대부분은 보통연금이다.
- 연금의 미래가치: FVA = A x {(1 + r)^n - 1} / r
- 연금의 현재가치: PVA = A x {(1 + r)^n - 1} / r * 1 /(1+r)^n
ex) 연간 120만 원씩 연간 복리이자가 6.5%인 저축에 납입할 때, 3년 후의 잔고는 얼마인가?
FVA = A x {(1 + r)^n - 1} / r = 1,200,000 x {(1 + 0.065)^3 - 1}/0.065
FVA = A x FVIFA = 120만 원 * 3.199
ex) 이자율이 5%일 때, 연간 80만 원씩 10년간 지급하는 연금의 현재가치는?
PVA = A x {(1 + r)^n - 1} / r * 1 /(1+r)^n = 800,000 * {(1 + 0.05)^10 - 1} / 0.05 * 1/(1 + 0.05)^10
PVA = A x PVIFA = 80만 원 x 7.721
- 유가증권의 가치평가
1. 자산의 가치평가
모든 자산의 가치평가는 기본적으로 현금흐름할인법(DCF)법을 적용할 수 있다.(미래 총 현금흐름을 적정한 할인율로 할인하여 구함)
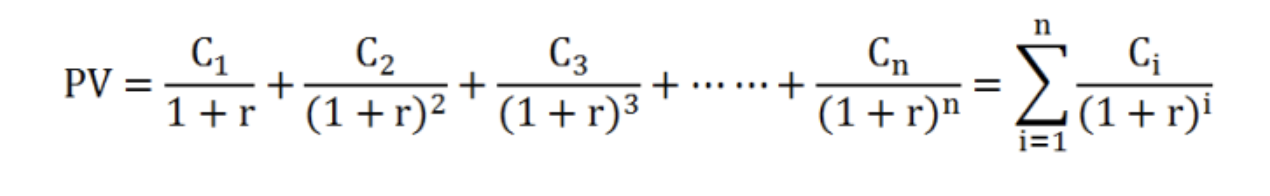
PV: 현재시점의 자산가치, Cn: 기간 n에서의 기대현금흐름, r: 요구수익률 또는 할인율, n: 보유기간의 길이
2. 이표채의 가치평가 - DCF법

CFn: 이자, TVn: 원금
3. 이표채의 가치평가 - 연금공식법
P = I x (PVIFA) + F x (PVIF)
(I는 이자, F는 원금)
4. 영구채권의 가치평가
영구채권은 만기가 없으므로 주식과 같이 평가한다.
I / K
표면이자 / 할인률
5. 우선주의 가치평가(제로성장모형)
I / K
배당 / 할인률
ex) 액면 10000원, 표면금리 6%, 만기 3년, 연단위후급 이표채를 만기수익률 4%로 발행일에 매입할 경우 매입가격은?
p1 = 600 / (1 + 0.04)
p2 = 600 / (1 + 0.04)^2
p3 = 10600 / (1 + 0.04)^3
p = p1 + p2 + p3 = 600 / (1 + 0.04) + 600 / (1 + 0.04)^2 + 10600 / (1 + 0.04)^3
ex) 액면 10000원, 표면이자율 6%, 만기 3년, 연단위후급 이표채를 발행일에 만기수익률 8%로 매입하고자 한다면 채권의 가격은?
P = I x PVIFA + F x PVIF
P = 10000 x 0.06 + {(1 + 0.08)^3 - 1} / 0.08 x 1/(1 + 0.08)^3 + 10000 x 1/(1 + 0.08)^3
ex) 채권의 액면가 10만 원, 표면금리 4%, 만기가 없는 무보증채, 연후급이표채, 만기수익률 6.25%일 때 채권의 가격은?
만기가 없으므로 영구채권이다. 따라서 배당 / 할인률 = 100,000 x 0.04 / 0.0625
- 보통주의 가치평가
1. 보통주의 가치평가가 가장 어려운 이유
- 자산의 현재가치(P)는 미래총현금흐름(S)을 적정한 자본할인율(r)로 n기간만큼 할인한 금액이 된다.
- 채권(확정이자부채권)은 S가 확정되어 있으므로 자본할인율(k)을 적정하게 추정하면 되지만(예금의 경우 무위험수익률이 할인율이 됨), 주식이나 부동산은 분자에 해당하는 미래현금흐름(S)의 추정이 매우 어렵다. 즉, 주식은 채권에 비해 밸류에이션이 매우 어렵다.
2. 배당평가 일반모형
P = D / k (P는 주식가치, D는 배당금, k는 요구수익률)
ex) 매기 배당금이 1,000원, 요구수익률이 10%일 경우 주식가치는?
P = D / k = 1,000 / 0.1 = 10,000원
3. 보통주의 가치평가를 위한 성장모형
- 제로성장모형(무성장모형)
미래배당금이 매 기간 일정하고 전혀 성장하지 않음.
P = D / k
- 정률성장모형(Gordon의 항상성장모형)
미래배당금이 매 기간 일정비율 g로 지속적으로 성장(요구수익률(k)이 배당성장률(g)보다 크다는 것을 전제. k > g)
P = D1 / (k - g) = D0(1 + g) / (k - g)
*항상성장모형은 분자가 D0 또는 D1에 따라 값이 달라지므로 주의. 예상배당금 처럼 예상이라는 표현이 들어가면 D1
ex) 전년도 주당배당금이 5,000원, 투자자의 요구수익률이 10%, 배당성장률이 5%로 추정될 때, Gordon의 성장모형으로 평가한 올해의 적정주가는?
P = D0(1 + g) / (k - g) = 5000(1 + 0.05) / (0.1 - 0.05)
* SML이론상 요구수익률과 자기자본비용은 같은 개념.
- 초기고속성장모형(다단계 성장모형)
초기에 정상적인 수준보다 훨씬 높은 성장률은 구가하다 급성장기간이 지나면 이익과 배당률은 안정을 되찾음.
4. 배당관련식
- 배당수익률 = 주당배당 / 주가 = D / P
- 배당성향 = 주당배당 / 주당순이익 = D / E = 1 - b (b는 유보율. 배당하고 남은 돈)
- 배당성장률 = 사내유보율 x 자기자본이익률 = g = b x ROE
- 요구수익률 k = 배당수익률 + 배당성장률 = D1 / P + g
'경제 > 투자자산운용사' 카테고리의 다른 글
| [투자자산운용사] 투자운용 및 전략 - 투자분석기법 - 3 (0) | 2023.12.19 |
|---|---|
| [투자자산운용사] 투자운용 및 전략 - 투자분석기법 - 2 (1) | 2023.12.19 |
| [투자자산운용사] 투자운용 및 전략 - 대안투자운용/투자전략 - 4 (0) | 2023.12.19 |
| [투자자산운용사] 투자운용 및 전략 - 대안투자운용/투자전략 - 3 (1) | 2023.12.19 |
| [투자자산운용사] 투자운용 및 전략 - 대안투자운용/투자전략 - 2 (0) | 2023.12.19 |